ПОСТАНОВКА ЗАДАЧИ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ

Основной задачей контура управления в системе те­леуправления, решающей задачу наведения, является обеспечение точности в момент встречи tB. Как отмеча­лось в 1.2, точность наведения может характеризоваться математическим ожиданием М от скалярной функции f вектора фазовых координат цели и наводящегося объек­та х в момент встречи. Таким образом, в качестве кри­терия качества контура управления I рассматривается функционал

I = M{Fx{tJ}. (2.1)

Вектор фазовых координат наводящегося объекта и це­ли х размерности пХ 1 удовлетворяет системе дифферен­циальных уравнений, которая в общем случае записыва­ется в виде

■*=/(*• и» h *); x{t0)=x°9 (2.2)

где х={х, х2,…, хп}у и nv —управляющие воздейст­вия на наводящийся объект и цель.

В частности, ей® могут являться ускорениями этих объектов или характеризовать углы отклонения рулей и т. д. В общем случае они являются векторами размерно­сти и(гХ1) иг»(тХ1).

Вектор случайных воздействий |(дХ1) характеризует возмущения, действующие непосредственно на наводя­щийся объект. В системе телеуправления §(£) является в основном следствием ошибок линии передачи команд и описывается белым шумом (1.3) с известной дисперсион­ной матрицей M(t):

М [1 &) 1г (*,)]=м (д 8 & — д. (2.3)

Значения вектора фазовых координат х в момент t0 являются случайными начальными условиями процессов наведения и имеют известные, статистические характери­стики.

Момент встречи tB определяется из условия миниму­ма дальности от наводящегося объекта до цели D:

D{tB)=M{D[x{t t)} (2.4)

t

на рассматриваемом интервале времени (/о,. Т), или ми­нимума функции в функционале (2.1).

Вектор управлений наводящегося объекта и в общем является детерминированным оператором от вектора из­мерений. г размерности (/X1). Управление будем считать физически осуществимым, если в момент t оно зависит лишь от значений Z, полученных в прошлые моменты вре­мени, т. е.

u = u(z(x), ./), х </. (2.5)

Вектор измерений содержит данные о фазовых коор­динатах наводящегося объекта и цели, получаемые ра­диолокаторами системы телеуправления, с ошибками п(/). Поскольку ошибки, являющиеся векторным белым шумом размерности (/XI) с корреляционной матрицей

м п (д »г(д]=лг(д ь (/,-д, (2.6)

содержат не только аддитивные, но и мультипликатив­ные составляющие, вектор z записывается в общем ви­де выражением

z=z(x, п, t).

Согласно 1.2 вектор управлений u(t), как и вектор <o(t), удовлетворяет «жестким» ограничениям

(2.8)

т. е. принадлежит замкнутой (имеющей фиксированную границу) области U и интегральным ограничениям в виде

(2.9)

где матрица q(t) (rXr) положительно-определенная.

Смысл условий (2.8) и (2.9) разъяснен в 1.2.

Контур управления будем называть оптимальным, если управляющее воздействие u(t) минимизирует кри­терий (2.1) и удовлетворяет ограничениям (2.8) и (2.9) при заданных статистических характеристиках случай­ных возмущений §(/) и n(t) и начальных условий дс(^о) •

При этом поведение цели может быть задано либо априорными статистическими характеристиками, либо оказывающим противодействие наводящемуся объекту в пределах ее энергетических и информационных возмож­ностей. В последнем случае цель, создавая организован­ные помехи, может изменять структуру вектора Z [см. выражение (2.7)] и выбирать закон управления t>(£) для увеличения критерия (2.1) [22].

Рассматриваемая задача оптимизации управления u(t) представляет собой специфическую вариационную задачу, особенность которой определяется зависимостью функционала / [см. выражение (2.1)] от момента встре­чи tB, который, в свою очередь, зависит от процесса на­ведения. В частном случае при заданном tB рассматривае­мая задача сводится к задаче управления конечным со­стоянием. Если, условие (2.4) совпадает с функционалом (2.1), то задача оптимизации является вариационной за­дачей с произвольным правым концом. Когда условие (2.4) может быть представлено в виде дифференциаль­ного или алгебраического соотношения, приходим к зада­че с условием трансверсальности на правом конце.

Сформулированную выше задачу при нефиксирован­ном виде зависимости управления « от вектора z назовем задачей оптимизации в произвольном классе управлений.

Большой практический интерес могут представлять также задачи оптимизации управления при частично или
полностью заданной структуре управления, т. е. при за­данном классе операторов, определяющих зависимость вектора и от измерений г и времени t. При этом опреде­ляются оптимальные значения постоянных величин или функции времени.

Многие принципиальные результаты для систем теле­управления могут быть получены при рассмотрении ли­нейной системы наведения. В этом случае система урав­нений (2.2) имеет вид

x=Ax—Buu—Bvv—V,
x(t$=x,

где А, Ви, Bv — матрицы размерности (пХп), (пХг) и и (пХт) соответственно, а вектор управлений и (г, t) является линейным оператором от вектора z

t

u{t)—w(t, x)z{x)dx, (2.11)

и

где w (t, т) матрица (г)<7) импульсных переходных функ­ций, определяемая при решении задачи. В линейной за­даче вектор z также предполагается линейной функцией фазовых координат

z=Cx—n. (2.12)

Матрица С в уравнении (2.12) размерности (ІХп) по­зволяет выделить из вектора х измеряемые в системе на­ведения фазовые координаты.

Для систем телеуправления характерна возможность сведения задачи к рассмотрению линейной стационарной системы наведения. В этом случае матрицы А, Ви, Bv и С являются постоянными, а

w(t, x)=w(t — x) сводится к функции. одной переменной.

2.1. УСЛОВИЯ ОПТИМАЛЬНОСТИ УПРАВЛЕНИЯ

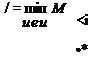Получим сначала необходимые условия оптимально­сти управления для фиксированного момента встречи tK и статистически заданного поведения цели v(t). Эта задача сводится к минимизации функционала

где математическое ожидание М означает среднее по начальным условиям лс°, возмущениям %(t) и n{t), а так­же управлениям дели v(t). Функция f0(x, и, v, t) учи­тывает интегральные ограничения на управления u(t).

Фазовые координаты x(t) удовлетворяют уравнениям (2.2), а функции /*, г=0, 1,… предполагаются непрерыв­ными ограниченными функциями своих аргументов и дважды дифференцируемыми по ж и и.

Ограниченность области U возможных значений уп­равлений и (t) вызывает трудности применения класси­ческих методов вариационного исчисления. Поэтому для решения этой задачи более удобно использовать методы динамического программирования или принцип макси­мума [3, 15].

Для получения условий оптимальности u(t) в форме уравнения динамического программирования обозначим

?!*(*), f = JVoC*. a, v, t)rfT + F [*(*„)]. (2.14)

t

Тогда

/=тіпМ[<р(лг(д, д]. (2.15)

а ви

Заменяя в выражении (2.14) t на t+At и вычитая его из (2.14), получим

<р[л:(^), f=yx(tkf),

<+д<

+ f /о(*. и» Ь т)Л. (2.16)

І

Пусть далее й обозначает момент начала измерений вектора г в выражении (2.7). В общем случае момент /о начала поступления информации не совпадает с мо­ментом t0 начала процесса управления, более того обыч­но К <t0.

Используем свойство условных математических ожи­даний, по которому предварительное усреднение при уве­личении объема заданной информации по сравнению с объемом информации при последующих усреднениях не

изменяет результата усреднения [12]. Математически этот факт выражает равенство

интервалах времени (to, І) и (to, т).

На основании соотношения (2.17) и учитывая, что в функционале (2.13) усреднение осуществляется при от­сутствии измерений, получаем, что минимум функциона­ла / будет обеспечен выбором управления, минимизиру­ющего функционал I при условном математическом ожи­дании

где использовано выражение (2.15). Обозначим далее

S(zJ. t /)=minAf Г<р(дг(0, 0І / 1

0 и*веи | Ьо |

значение функционала, получаемого выбором значений управления на интервале (i, tB) при полученных измере­ниях до момента £ Тогда минимизируемый функционал (2.18) может быть представлен в виде

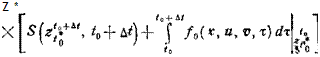(2.20)

При получении зависимости (2.20) использовано выра­жение (2.16), свойство условных математических ожида­ний по отношению к функции ф(*(/о+Л£), to+’&t) и факт независимости второго слагаемого в правой части (2.16) от значений управлений на интервале (/+Д/, tB). Как обычно при получении уравнения Беїллмана, момент t$ яв-

ляется произвольным, поэтому условие оптимальности управления и зависимости (2.20) должно быть выпол­нено для произвольного t интервала управления:

[<+д< і — і

* + Д*) + j /<>(•*> *, T)rfTLj* • (2-21)

Необходимое условие оптимальности (2.21) является функциональным уравнением, решение и исследование его — трудная задача. Поэтому преобразуем это условие к форме принципа максимума, что позволяет в ряде за­дач использовать приближенные методы решения. Для этого запишем уравнение (2.21) в виде равенства

min М [<р (х {t -[- Д/), — 9(^(0» 0“Ь

(2.22)

^{x{t + Li),t + Lt)-^{x{t),t)= f x)-dx. (2.23)

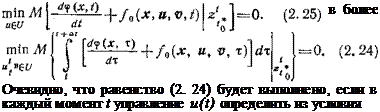J ‘ dX

Из определения полной производной

Обозначим через ф(/) вектор-функцию размерности (rt-HXl) с элементами

%=-U

(

___ О

dt

и введем стохастический гамильтониан, равный скаляр­ному произведению

Н{х, ф, и, vx 0= ФТ(*)/(*. и, 0. (2.28)

где вектор / имеет размерность (п+ 1X0 ‘>

f{x, », г», 0={/о(*> И, Я, 0, Л(*. и, V, t), 1), (2.2Э)

где f(x, и, v, t) вектор («Х1)> составляющий правую часть системы (2.2).

Используя выражение (2.16), можно переписать ус­ловие оптимальности управления (2.13) в форме стоха­стического принципа максимума

Вектор ф(/) может быть определен системой уравнений аналогично принципу максимума в детерминированном случае [13]. Дифференцируя выражение (2.27), получим

где -2? ^—матрица (п X «) с элементами ——————— .

ахах ox fix j

Согласно определению функции (р(лг, t) [см. выражение (2.14)] и соотношению для полной производной (2.26), получим

—- (2.32)

Подставляя выражение (2.32) в соотношение (2.31), на­ходим

или, учитывая обозначение (2.28),

_ ^Td/U. и» v> О dt дх

Система п дифференциальных уравнений (2.33) совпада­ет с системой уравнений для сопряженных функций в де­терминированном случае принципа максимума [15]. На­чальные условия для этой системы могут быть найдены из выражений (2.27). При t=tb

(2.35)

и вектор

♦ СО = —У ■ (2-36)

VX Ub)

Особенность рассматриваемой статической задачи по сравнению с детерминированной состоит в том, что га­мильтониан Н(х, ф, u, v, t) и функции ip(t) являются слу­чайными, а система уравнений (2.33) стохастической системой дифференциальных уравнений. Поэтому числен­ные методы к решению этой задачи могут быть примене­ны лишь в частных случаях, что существенно усложня­ет процедуру получения оптимального управления и.

Поскольку гамильтониан Я является функцией от — значения управления и в момент t, которое зависит от реализации z лишь на интервале наблюдения до момен­та t, управление u(t) в формуле (2.30) является неслу­чайным по отношению к условному математическому ожиданию и может быть вынесено за его знак. Операция усреднения применяется в условии оптимальности (2.30) по отношению к функциям /(ц, х, V, |, t), ф и х. Резуль­тат усреднения формулы (2.30) не зависит от перемен­ных ф и х, а является функцией только наблюдаемых ве­личин z на интервале (^о, t). Поэтому управление

u(t), определенное из формулы (2.30), также будет за­висеть только от полученных значений вектора г на ин­тервале (^о, t) и будет удовлетворять условию физиче­ской осуществимости (2.5).

Условия оптимальности (2.21) и (2.30) эквивалент­ны, поскольку они вытекают одно из другого, и являют­ся необходимыми условиями оптимальности управления u(z, t) в том смысле, что могут быть получены на основе исследования первой вариации функционала / и не учи­тывают характера вариации I второго порядка.

Выше предполагалось, что момент встречи tB изве­стен. В задачах наведения момент tB можно рассматри­вать как функцию фазовых координат, определяемую условием типа (2.4). Если это условие может быть вы­ражено в виде алгебраического или дифференциального соотношения вида

D(x, и, tB)=c, (2.37)

то его можно рассматривать как ограничение на значе­ния фазовых координат и момент встречи tB. Учет такого типа условий в вариационном исчислении осуществляет^ ся с помощью условий трансверсальности [6]. Уравнения оптимальности (2.21) и (2.30) при этом остаются в силе, а граничные условия (2.36) на сопряженные переменные ф(£) изменяются.